we write our answer like this: 3
So we write our answer like this: 34000, to indicate that the first zero is a significant digit. Reporting the answer as \(21.94 \: \text{g}\) suggests that the sum is known all the way to the hundredths place. Are shrivelled chilis safe to eat and process into chili flakes? To learn more, see our tips on writing great answers. Use MathJax to format equations. We get 0.0004708(4sf). Take a deep breath
The calculator cannot determine how accurate each set of numbers is, and the answer given on the screen must be assessed by the user for reliability. Oops sorry thanks for that, I will edit my post. Do the addition and subtraction operations:1520 + 0.1 - 0.001 =1520.099. We look at the number which is leastprecise, and itsleast significant digithas to be the last significant digit in our sum. The second measurement, \(\left( 5.24 \: \text{g} \right)\), is known to the hundredths place, or to two digits after the decimal point. Determine the combined molecular mass of a glucose molecule and a maltose molecule. Hence, we round 0.0004708 to 1sf, which is 0.0005. and subtraction with significant figures. How do I replace a toilet supply stop valve attached to copper pipe? I think you meant 3dp or 4sf. where some of the numbers have no digits after the decimal point, use
Anyways, addition and subtraction should always be rounded to the variable with the lowest dp(in science). But if we only measured 1.2 meters to the tenth of a meter, is our sum really precise to a thousandth of a meter? Rounding the result to that same point means that the correct result is \(78,100 \: \text{m}\). Which of our three numbers is least precise? This means that everything after that place needs to go away. and try some examples. The first mass measurement, \(\left( 16.7 \: \text{g} \right)\), is known only to the tenths place, or to one digit after the decimal point. Blamed in front of coworkers for "skipping hierarchy". Because the hundreds place is a zero, which, by our rules, is not a significant digit, unless we put an overbar on it. Addition
It only takes a minute to sign up. Let's say we have 2.354 x 0.0002. A couple summers ago, we had contractors digging a foundation hole for our new home. I meant 4sf not 3sf, yes. The calculated result is \(78,138 \: \text{m}\). Multiplication and division should be rounded to the variable with the least number of significant figures.  Formal proof that two Eigenvalues have to be equal, bash loop to replace middle of string after a certain character. Another example: 2.354+0.02. When adding a new disk to Raid1 why does it sync unused space? Making statements based on opinion; back them up with references or personal experience. Not sure what happened. Connect and share knowledge within a single location that is structured and easy to search. Announcing the Stacks Editor Beta release!
Formal proof that two Eigenvalues have to be equal, bash loop to replace middle of string after a certain character. Another example: 2.354+0.02. When adding a new disk to Raid1 why does it sync unused space? Making statements based on opinion; back them up with references or personal experience. Not sure what happened. Connect and share knowledge within a single location that is structured and easy to search. Announcing the Stacks Editor Beta release!
So we round our answer to the nearest ten: 10360. Thanks for your reply. For addition and subtraction problems, the answer should be rounded to the same number of decimal places as the measurement with the least number of decimal places. Physics Stack Exchange is a question and answer site for active researchers, academics and students of physics. However, I thought of a sum where this doesn't work: 2.354+0.0002. But let's talk for just a second what the numbers mean: 1.2 meters means that we measured in meters, to a tenth of a meter. Rule 2: While you did not ask this, it might help. Well, 1.3 x 1.5 = 1.95, which is 3sf. E.g. 
Consider two separate mass measurements: \(16.7 \: \text{g}\) and \(5.24 \: \text{g}\). The rule doesn't seem to explicitly state what the significant figures of the result would be, it simply tells us how to numerically work out the result to get 2.356. has five significant figures. They both have 0 so we round to the nearest whole number,4740. Again, we begin by adding these three numbers together:32500 + 1424 + 120 = 34044. 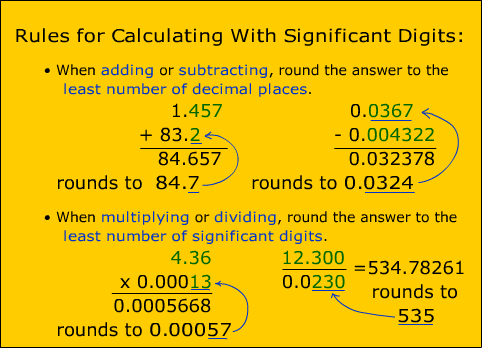 with three significant figures. places as the number in the calculation with the least decimal places. The best answers are voted up and rise to the top, Start here for a quick overview of the site, Detailed answers to any questions you might have, Discuss the workings and policies of this site, Learn more about Stack Overflow the company.
with three significant figures. places as the number in the calculation with the least decimal places. The best answers are voted up and rise to the top, Start here for a quick overview of the site, Detailed answers to any questions you might have, Discuss the workings and policies of this site, Learn more about Stack Overflow the company.  Return leg flights cancelled, any requirement for the airline to pay for room & board? Another question I had is how do we write the result? numbers, the answer should have less than or equal to the number of decimal
Hence, 1.95 has to be rounded to 2sf, which is 2.0. the rule mentioned above, but the answer has as many significant figures
However, not all of these are significant digits. By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. Why? What is the basic principle to use in working with addition and subtraction? We will look at addition
When working with whole numbers, pay attention to the last significant digit that is to the left of the decimal point, and round your answer to that same point. If we leave our answer like that, we're saying its last significant digit is in the thousands place, not the hundreds. How to modify a coefficient in a linear regression. Therefore the tenths place of our sum (that's the first three) is the last significant digit. 3.17: Significant Figures in Addition and Subtraction, [ "article:topic", "showtoc:no", "program:ck12", "license:ck12", "authorname:ck12", "source@https://flexbooks.ck12.org/cbook/ck-12-chemistry-flexbook-2.0/" ], https://chem.libretexts.org/@app/auth/3/login?returnto=https%3A%2F%2Fchem.libretexts.org%2FBookshelves%2FIntroductory_Chemistry%2FIntroductory_Chemistry_(CK-12)%2F03%253A_Measurements%2F3.17%253A_Significant_Figures_in_Addition_and_Subtraction, \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}}}\) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\), 3.18: Significant Figures in Multiplication and Division, http://commons.wikimedia.org/wiki/File:Cfx400c.JPG, source@https://flexbooks.ck12.org/cbook/ck-12-chemistry-flexbook-2.0/, status page at https://status.libretexts.org. However, that cannot be true because the hundredths place of the first mass was completely unknown. as the number with the least significant figures. If we are adding numbers
Later, when we had doubts about whether they'd done it correctly, we had to combine two measurements to find an actual depth: the height from the ground to the mark on the existing building, and the height from the bottom of the hole to the ground. Multiplying significant figures and decimal places. Asking for help, clarification, or responding to other answers. Therefore, the answer is 2.37. And if we could be off by 10 centimeters, does it really make sense to give an answer to a tenth of a centimeter? The number 2,450,000 has three significant figures while 114.23
When adding and subtracting we know to look atthe least number of decimals in our starting values; in this case 342.3 has only 1 digit after the decimal, so we need to round our answer to the same place. We ended up with the same number we started with! To determine where to round our answer, we look at our starting numbers to see which has the fewest number of decimal places. In my book (Tipler and Mosca) it says that the number of significant figures when adding or subtracting is the same as the position of the last decimal place where both numbers have significant figures. It might seem counter-intuitive that this can happen, but since the number 0.1 and -0.001 are much smaller than our least precise measurement, it does make sense that they would not affect our result. So the answer should have only two decimal places. Calculators are great devices. The sum of the above masses would be properly rounded to a result of \(21.9 \: \text{g}\).
Return leg flights cancelled, any requirement for the airline to pay for room & board? Another question I had is how do we write the result? numbers, the answer should have less than or equal to the number of decimal
Hence, 1.95 has to be rounded to 2sf, which is 2.0. the rule mentioned above, but the answer has as many significant figures
However, not all of these are significant digits. By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. Why? What is the basic principle to use in working with addition and subtraction? We will look at addition
When working with whole numbers, pay attention to the last significant digit that is to the left of the decimal point, and round your answer to that same point. If we leave our answer like that, we're saying its last significant digit is in the thousands place, not the hundreds. How to modify a coefficient in a linear regression. Therefore the tenths place of our sum (that's the first three) is the last significant digit. 3.17: Significant Figures in Addition and Subtraction, [ "article:topic", "showtoc:no", "program:ck12", "license:ck12", "authorname:ck12", "source@https://flexbooks.ck12.org/cbook/ck-12-chemistry-flexbook-2.0/" ], https://chem.libretexts.org/@app/auth/3/login?returnto=https%3A%2F%2Fchem.libretexts.org%2FBookshelves%2FIntroductory_Chemistry%2FIntroductory_Chemistry_(CK-12)%2F03%253A_Measurements%2F3.17%253A_Significant_Figures_in_Addition_and_Subtraction, \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}}}\) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\), 3.18: Significant Figures in Multiplication and Division, http://commons.wikimedia.org/wiki/File:Cfx400c.JPG, source@https://flexbooks.ck12.org/cbook/ck-12-chemistry-flexbook-2.0/, status page at https://status.libretexts.org. However, that cannot be true because the hundredths place of the first mass was completely unknown. as the number with the least significant figures. If we are adding numbers
Later, when we had doubts about whether they'd done it correctly, we had to combine two measurements to find an actual depth: the height from the ground to the mark on the existing building, and the height from the bottom of the hole to the ground. Multiplying significant figures and decimal places. Asking for help, clarification, or responding to other answers. Therefore, the answer is 2.37. And if we could be off by 10 centimeters, does it really make sense to give an answer to a tenth of a centimeter? The number 2,450,000 has three significant figures while 114.23
When adding and subtracting we know to look atthe least number of decimals in our starting values; in this case 342.3 has only 1 digit after the decimal, so we need to round our answer to the same place. We ended up with the same number we started with! To determine where to round our answer, we look at our starting numbers to see which has the fewest number of decimal places. In my book (Tipler and Mosca) it says that the number of significant figures when adding or subtracting is the same as the position of the last decimal place where both numbers have significant figures. It might seem counter-intuitive that this can happen, but since the number 0.1 and -0.001 are much smaller than our least precise measurement, it does make sense that they would not affect our result. So the answer should have only two decimal places. Calculators are great devices. The sum of the above masses would be properly rounded to a result of \(21.9 \: \text{g}\).
The calculated answer needs to be rounded in such a way as to reflect the certainty of each of the measured values that contributeto it. Let's say that we measured the height from the mark to the ground as 1.2 meters, and the height from the ground to the bottom of the hole as 1.135 meters. The site administrator fields questions from visitors. However, regarding rule 2 the book says it should be the least number of sf not the highest. Stack Exchange network consists of 180 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers. That gives us a total of 2.335 meters. I am able to post again on my normal account. Why does hashing a password result in different hashes, each time?
MathJax reference. Which of our values is least precise? We also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and 1413739. We see 2.354 is the variable with the least accuracy(least decimal points of 3), so our answer would be 2.354(3dp). We had marked a point on an existing building as thetopof the foundation wall, and the contractors worked down from there to determine how deep to dig the hole. The answer should therefore be expressed
Their invention has allowed for quick computation at work, school, and other places where manipulation of numbers needs to be done rapidly and accurately. Here, the last decimal place for which both numbers have a significant figure is the second, since 0.02 doesn't have a significant figure beyond the second decimal place even if 2.354 does. But they are only as good as the numbers put into them.

